Illustrated Guide to Cost Allocation
This describes the naive, direct, step, and reciprocal methods of cost allocation in modern accounting.
By Chris Niemira for BUSI611 at R.H. Smith School of Business, University of Maryland
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
This is what we've got:
- A company with four departments
- Two service, two production
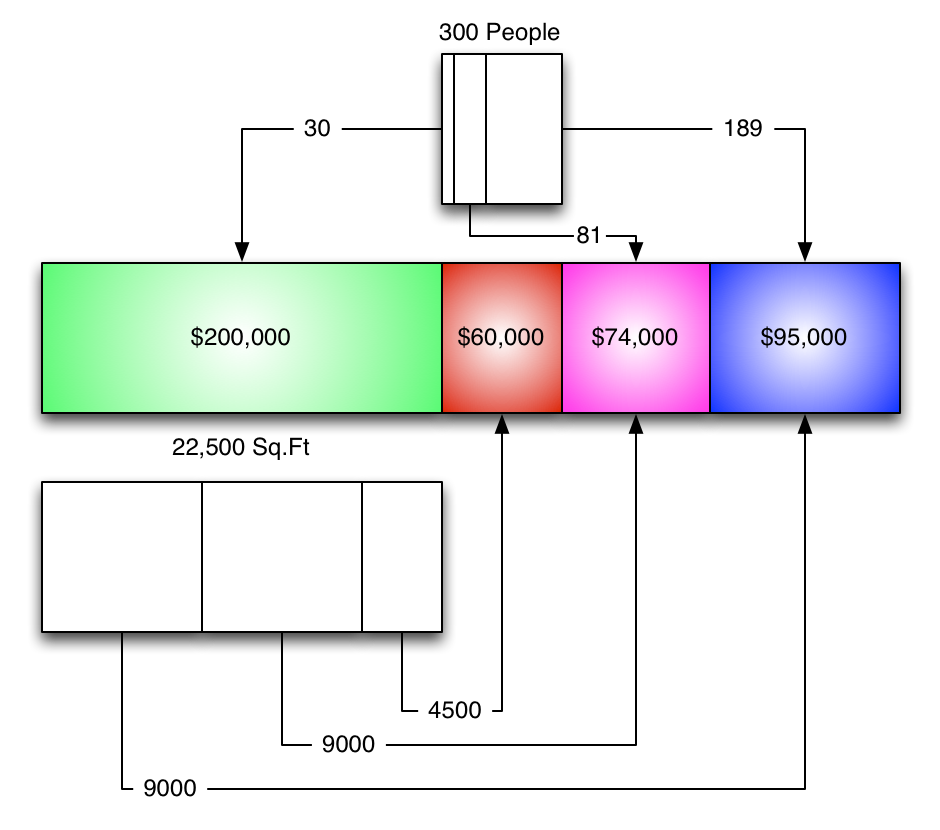
- Costs per department
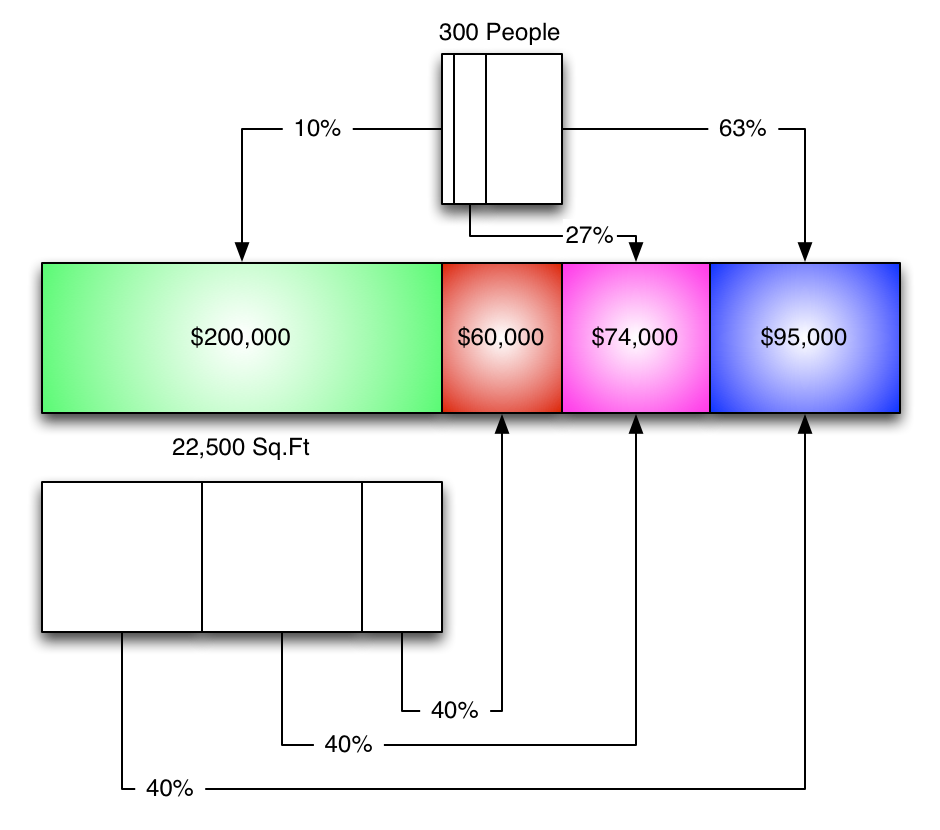
- Allocation rates for the service departments
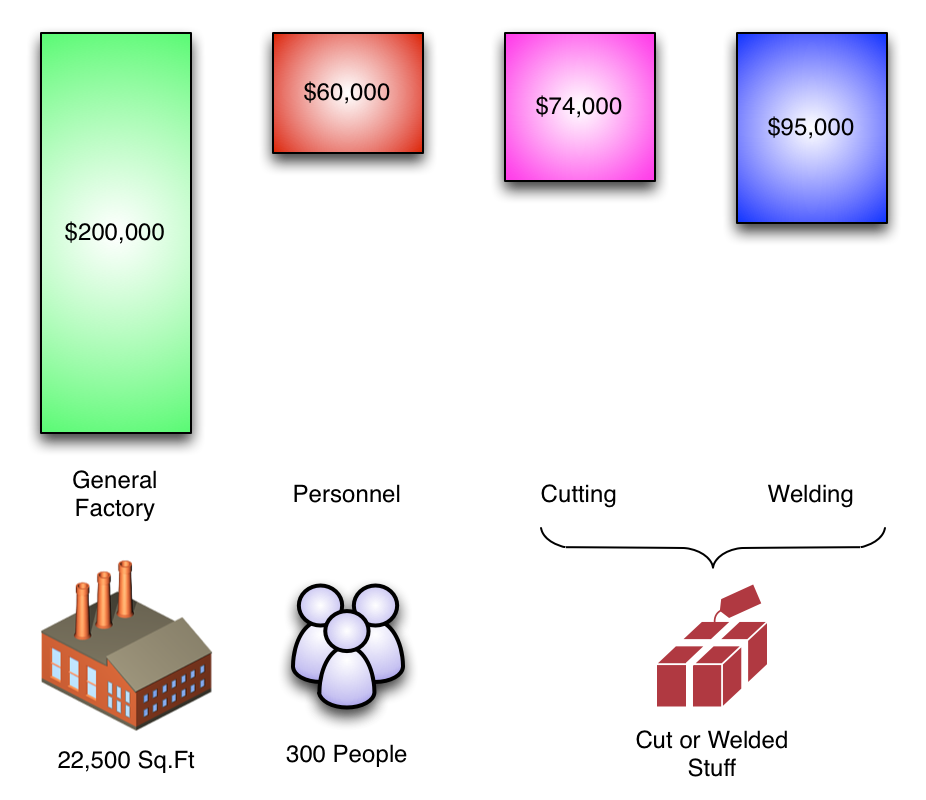
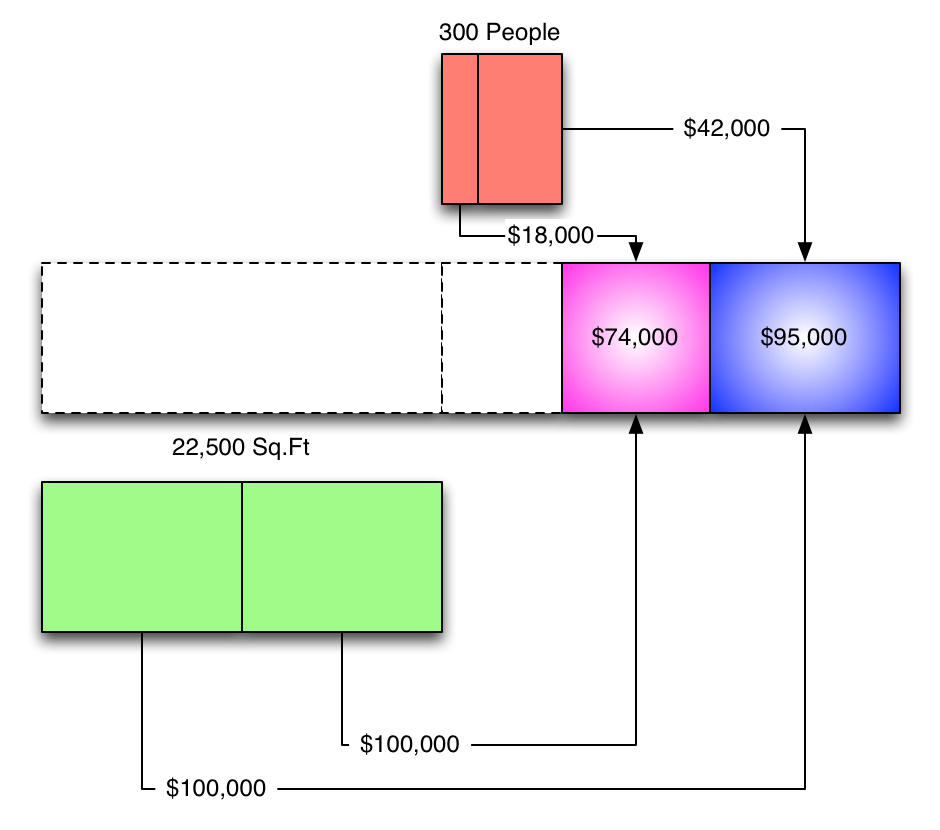
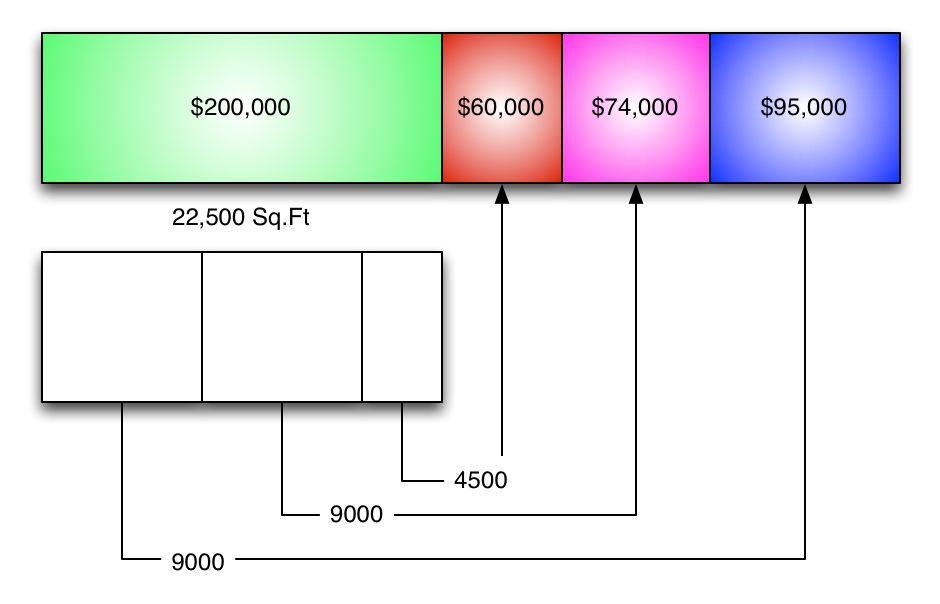
Expressed another way, it looks like this:
(Yes, all of the boxes are to scale.)
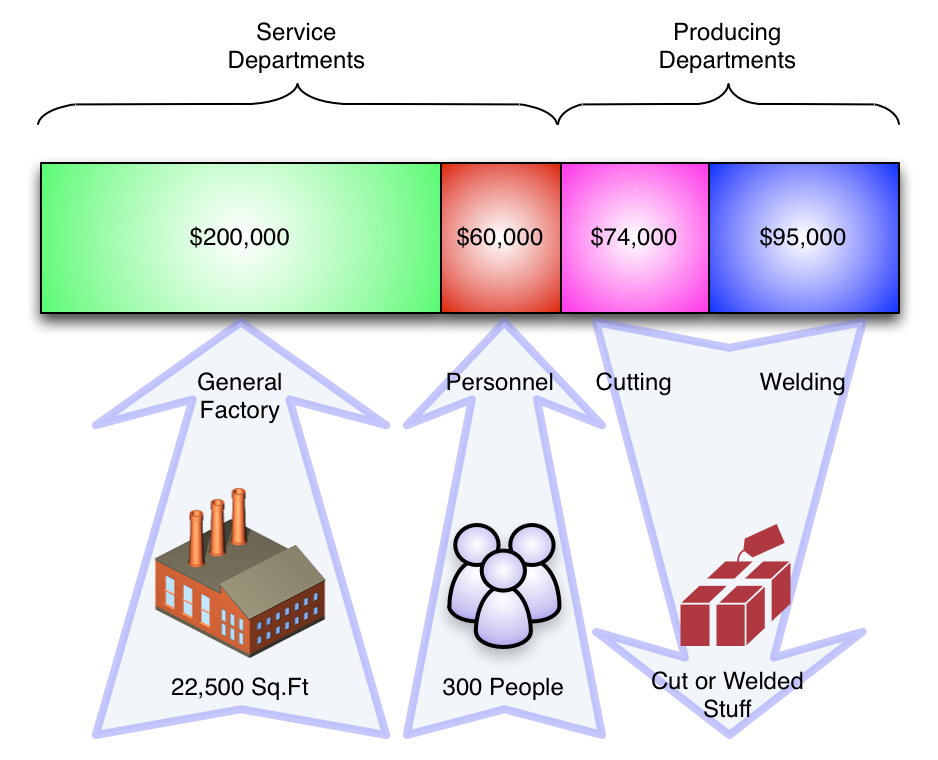
The goal is to allocate the service costs to the production departments (so they can be factored into COGS).
(BTW - that's because the service departments generate costs, but not revenue.)
In other words, we want to move all of the green and red dollars into the purple and blue categories.
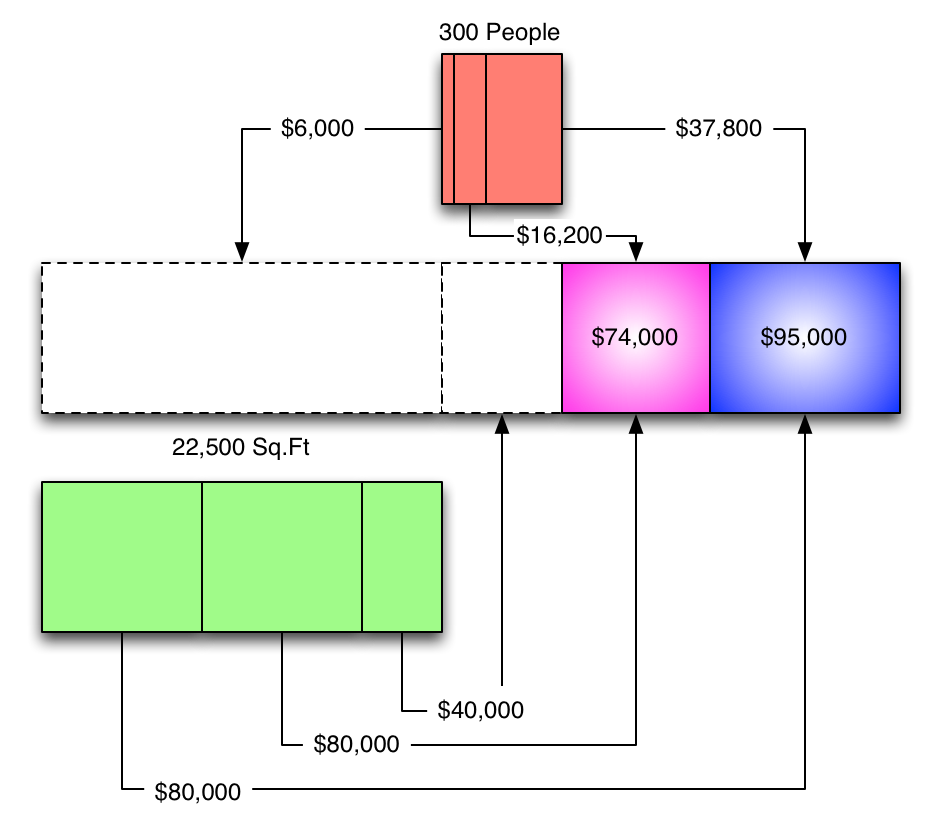
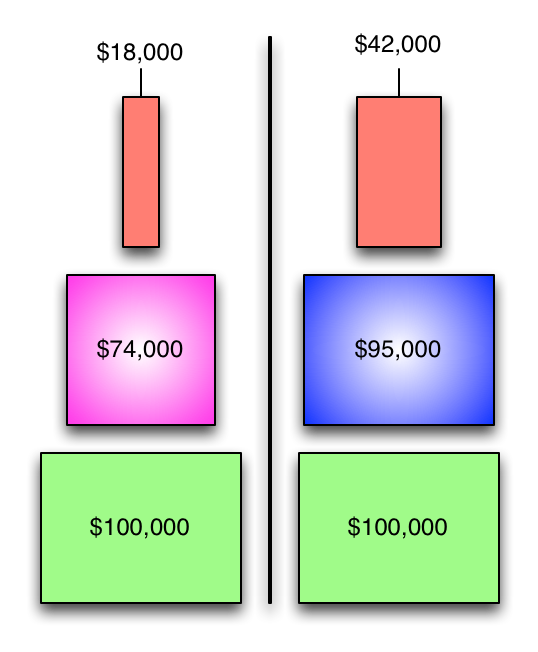
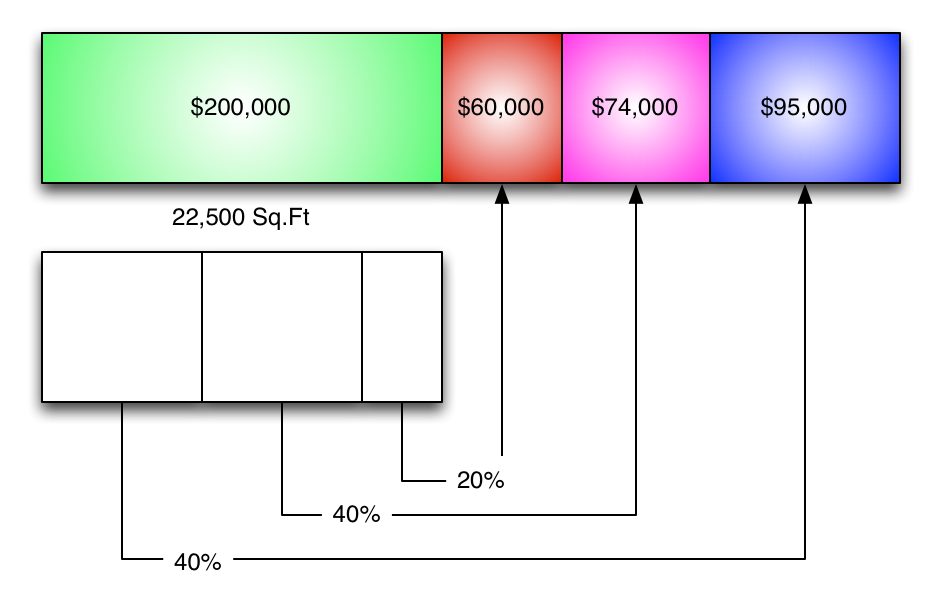
Visually, the cost allocations for the service departments look like this:
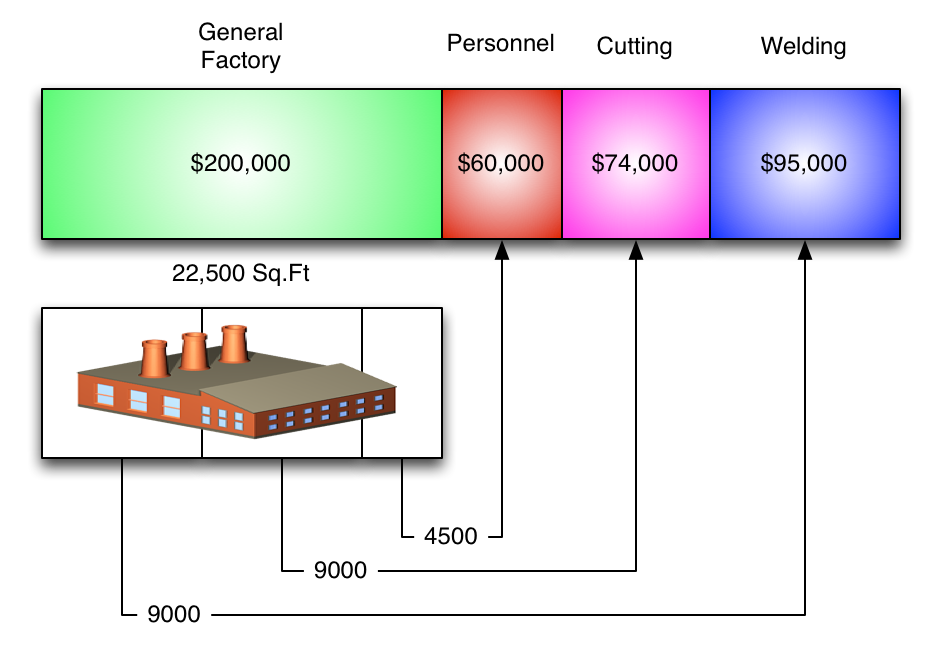
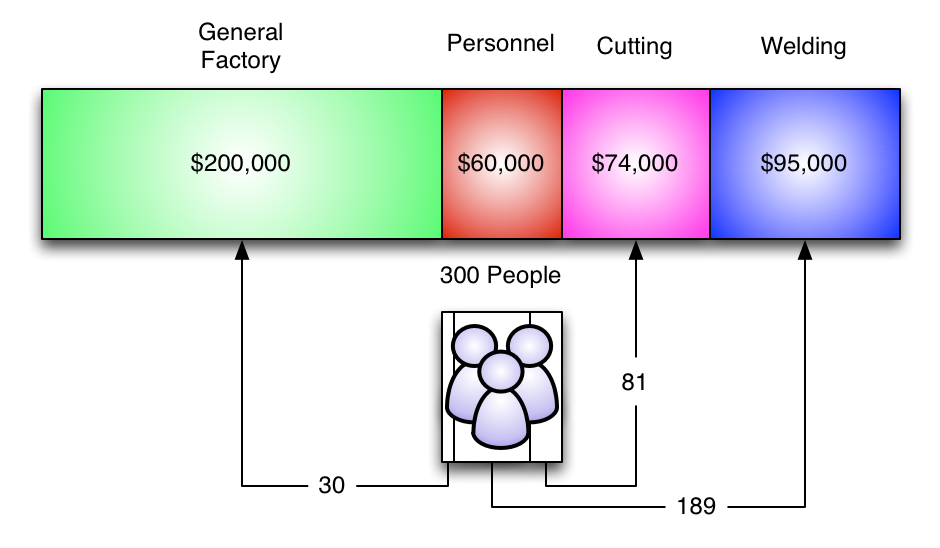
One way to do it is to simply chop up the service department allocations by percentages...
...then transfer the costs to their new departments...
...add 'em up, and...
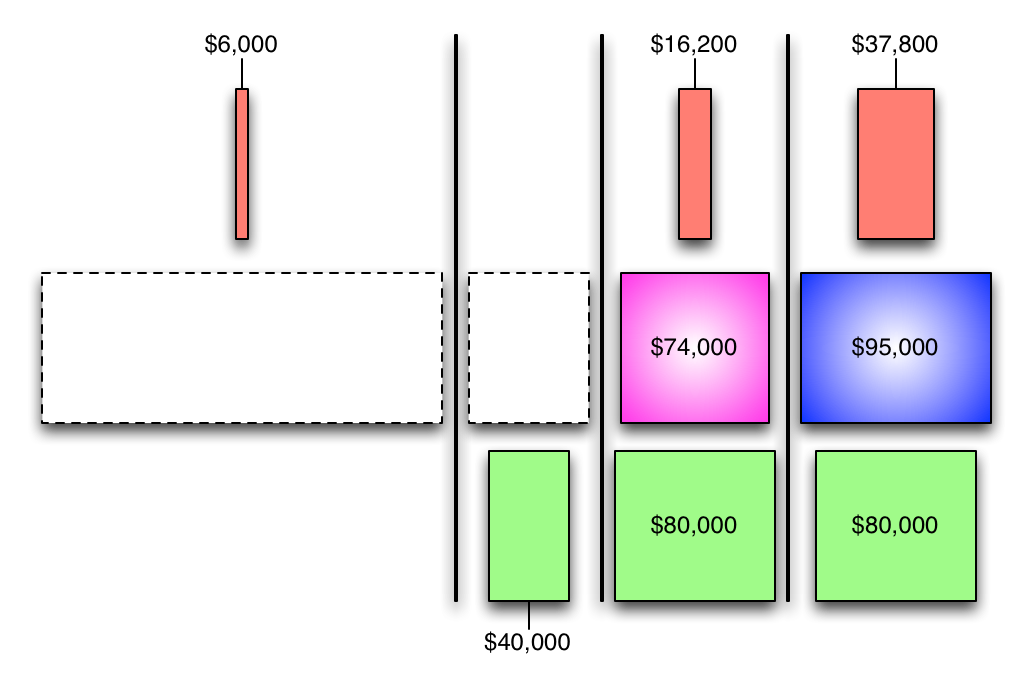
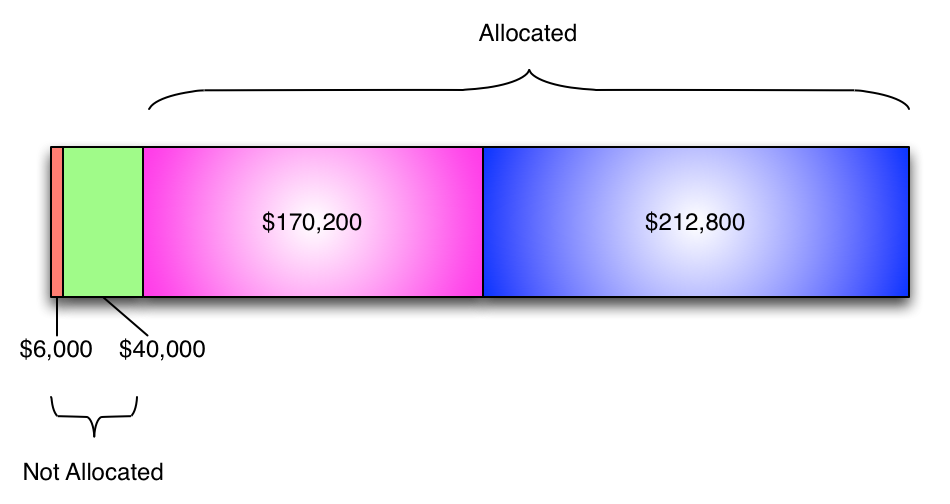
Hmm... that didn't work at all.
We ended up with $46,000 that didn't get allocated to production because each of the two service departments had some allocation to the other that we just ignored.
So let's try that again.

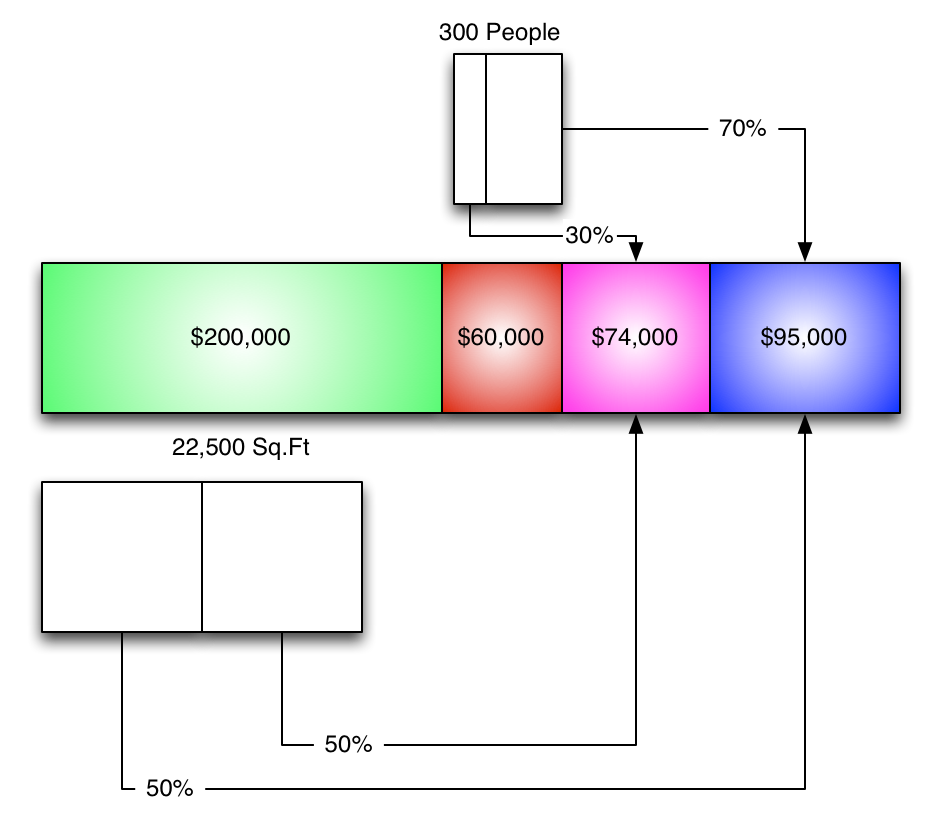
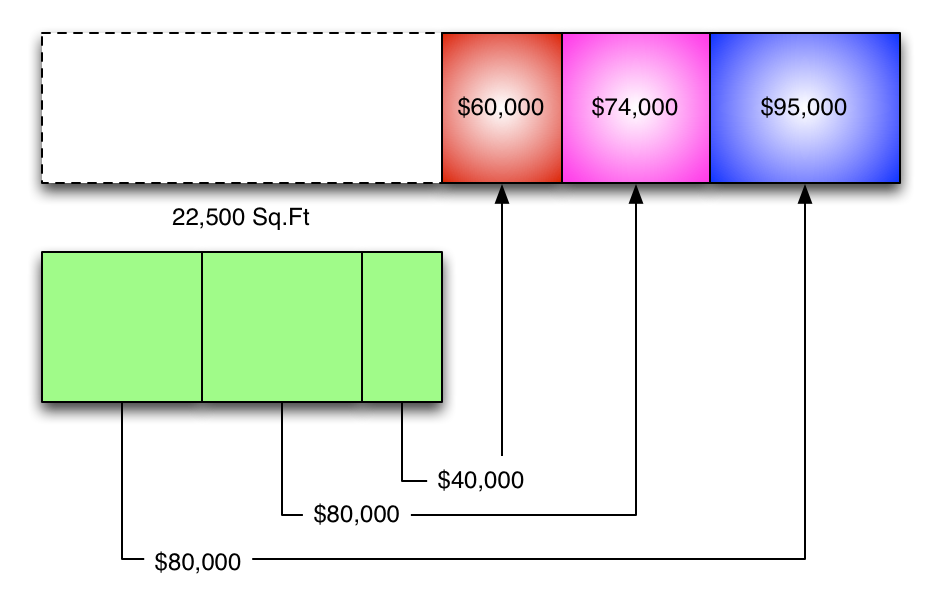
What if we just throw out the service-to-service allocations?
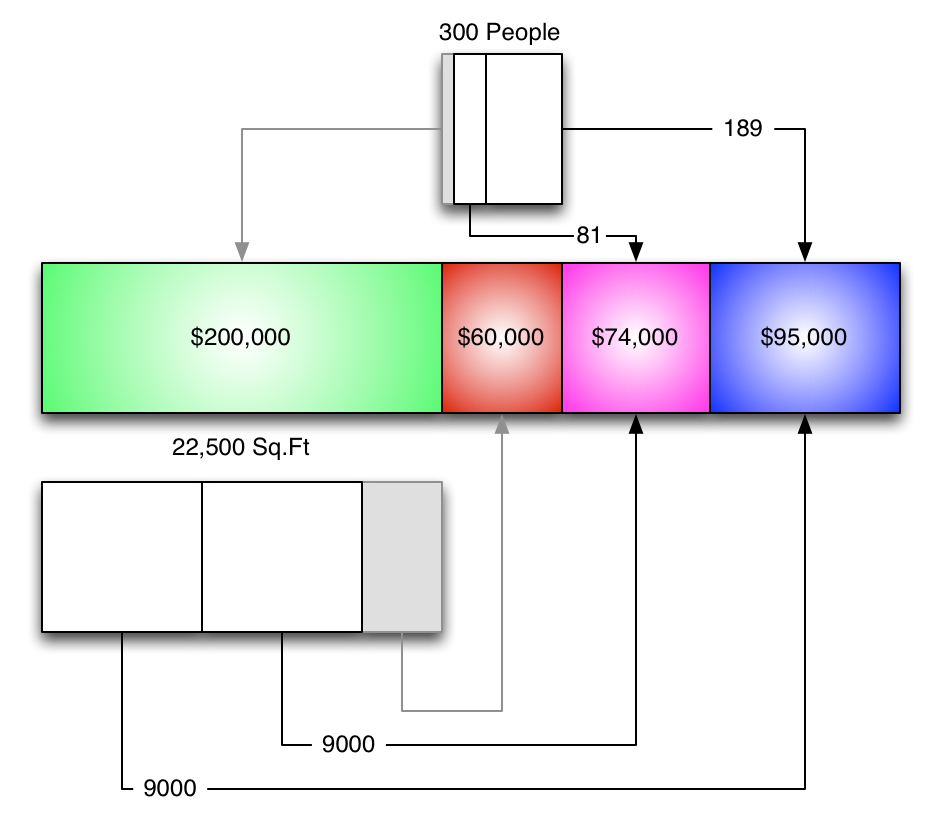
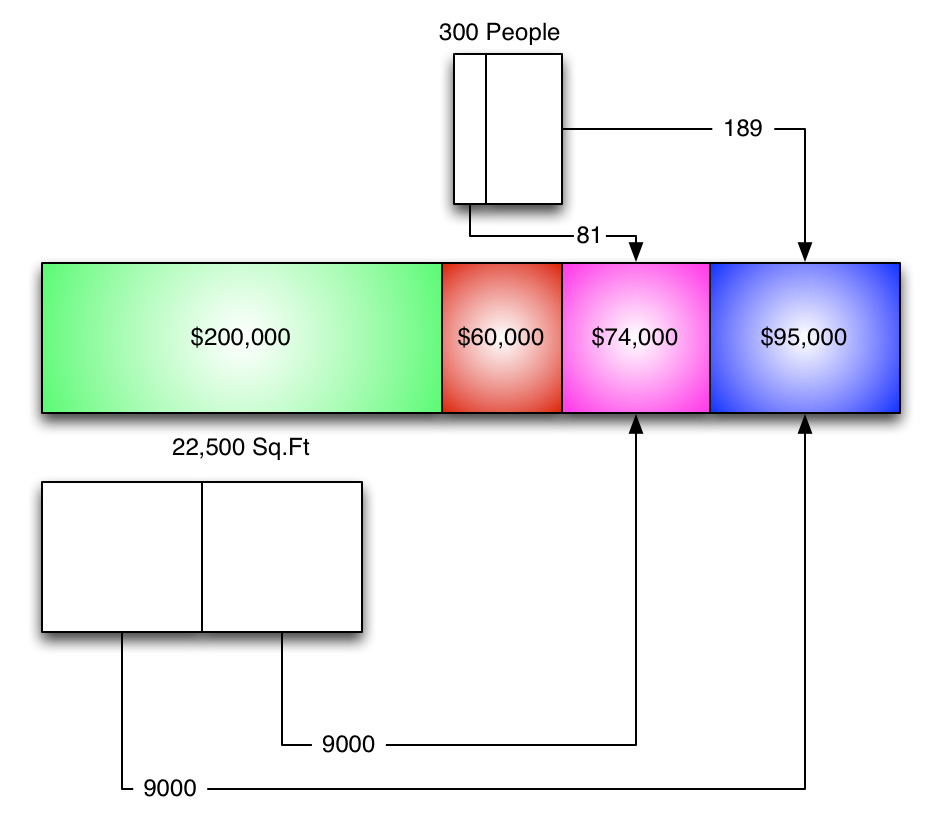
We can come up with new percentages and go from there.
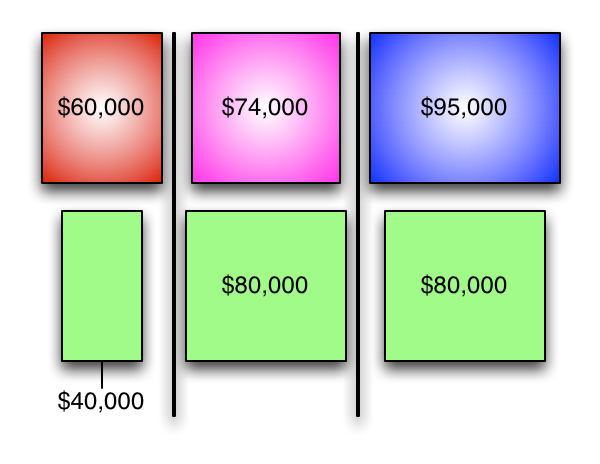
And now all of the costs are all allocated to production departments.
This is the "direct method."
It's okay, but since we threw out some of the numbers we can probably do better.
So, let's give it another go!

Let's put the smaller service allocation aside for the moment. Remember, red is just the "personnel" department.
(The HR types can usually wait.)
First, we'll knock out the "general factory" (green) allocation.
(Okay, actually the reason we're doing green before red is that "general factory" has a larger allocation to "personnel" than vice versa.)
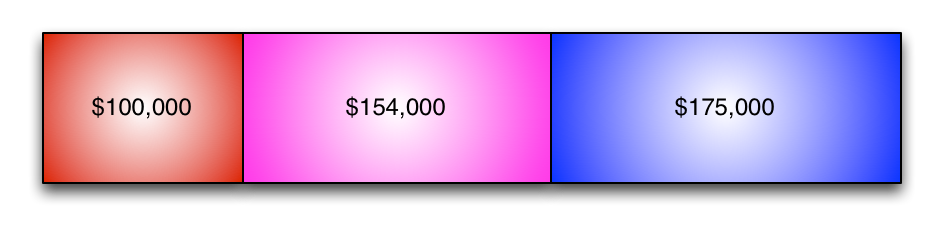
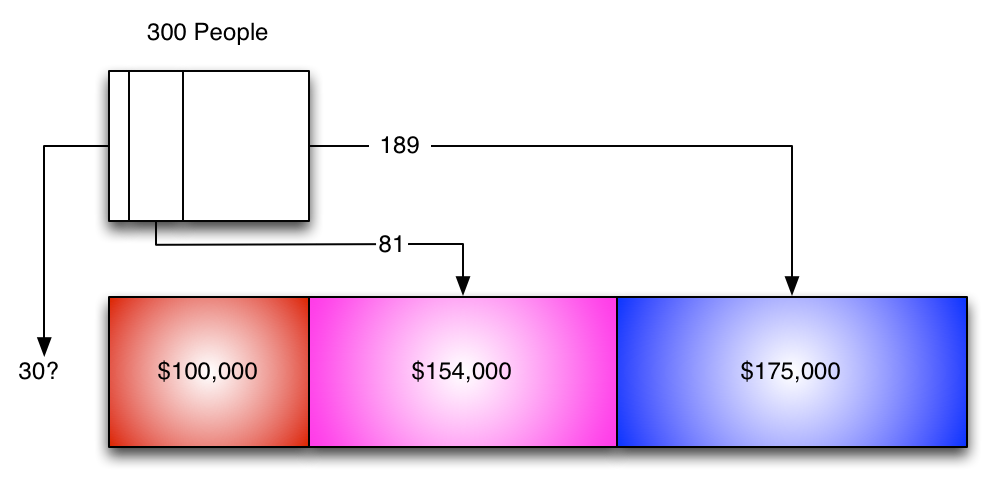
Now we can take a look at the "personnel" department and allocate its cost to production.
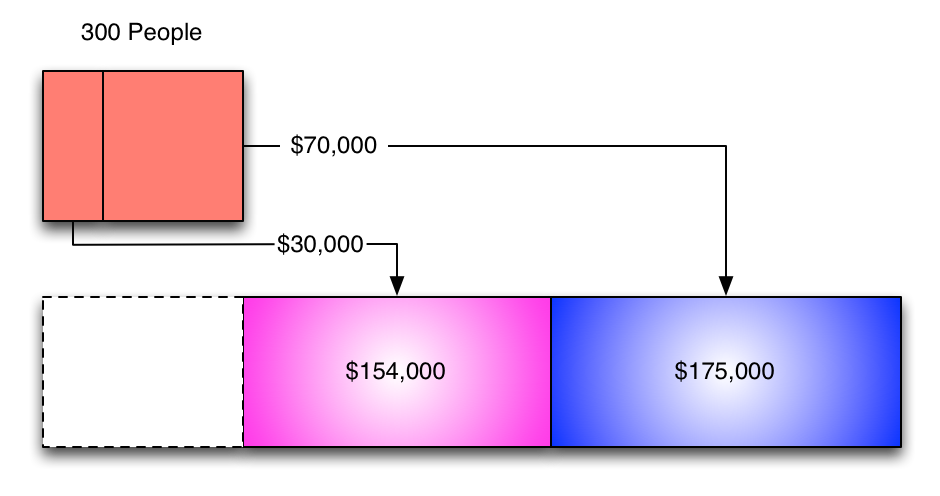
Uh oh.
10% of the costs for "personnel" are attributed to something that's already been dealt with.
So we throw it out, and come up with new percentages.

(At least now we're only fudging one number instead of two. Let's see if it pans out any better.)
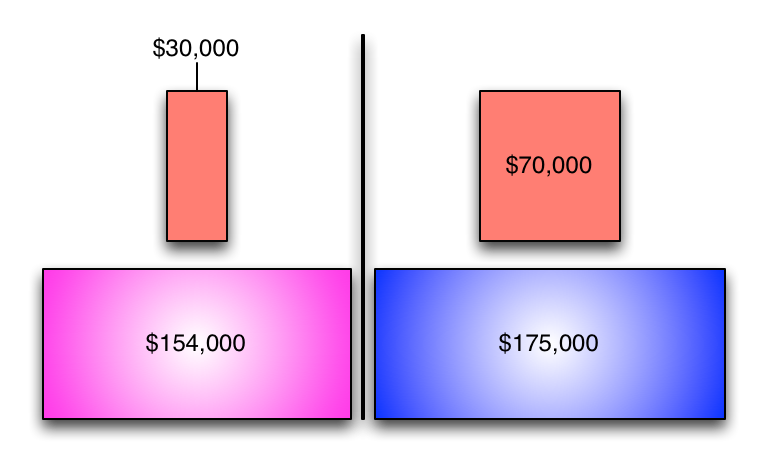

Well we got different numbers, but everything still worked out in the end.
That was the "step method" of cost allocation.
But we still threw out one of our numbers.
That means we can still do better.
Once more:

Let's keep a closer eye on the values we're dealing with this time...

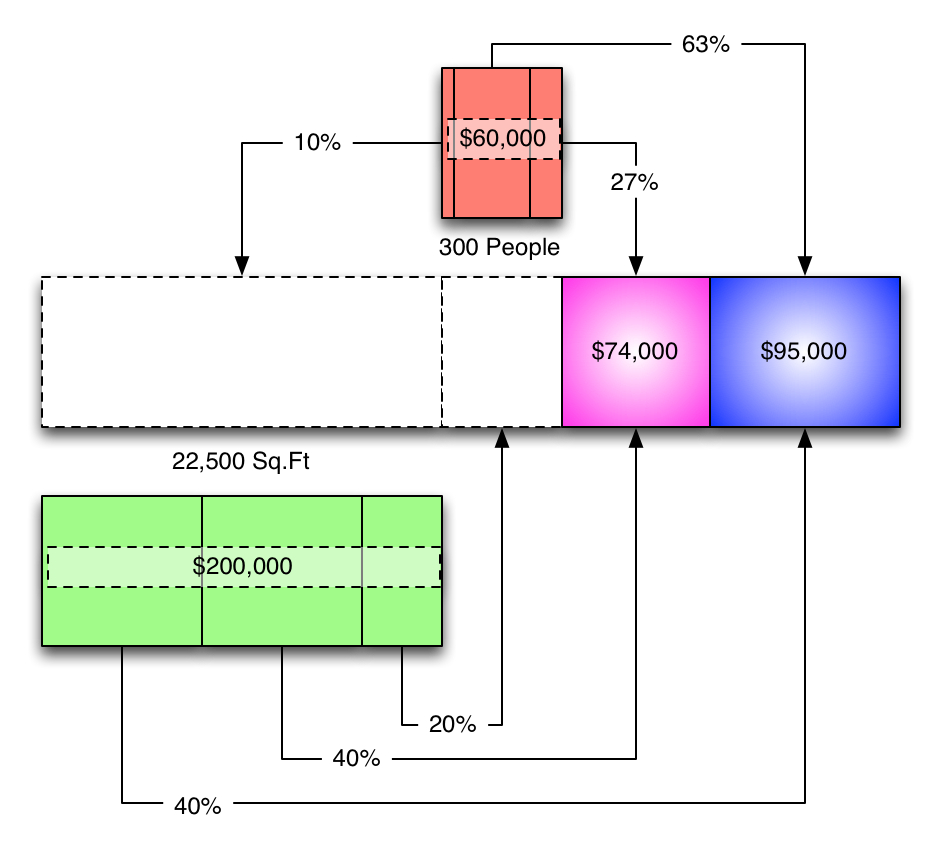
...because we're going to deal with the mutual service-to-service allocations.
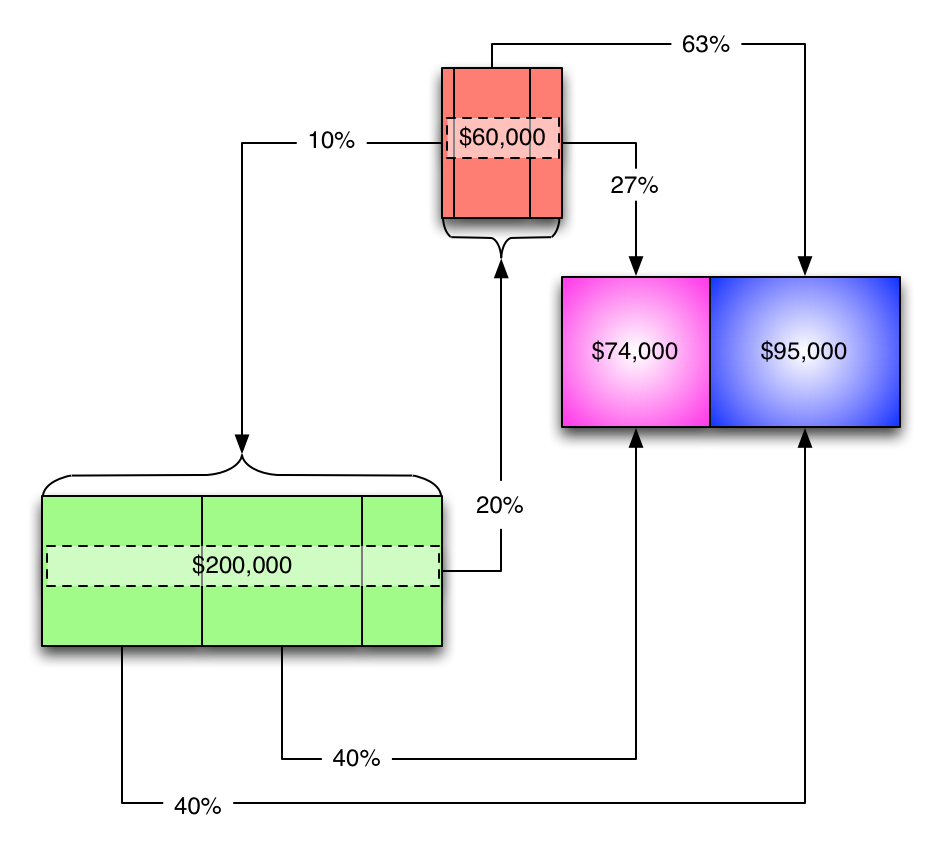
In fact, let's put aside the service-to-production allocations for the moment and deal just with the services...
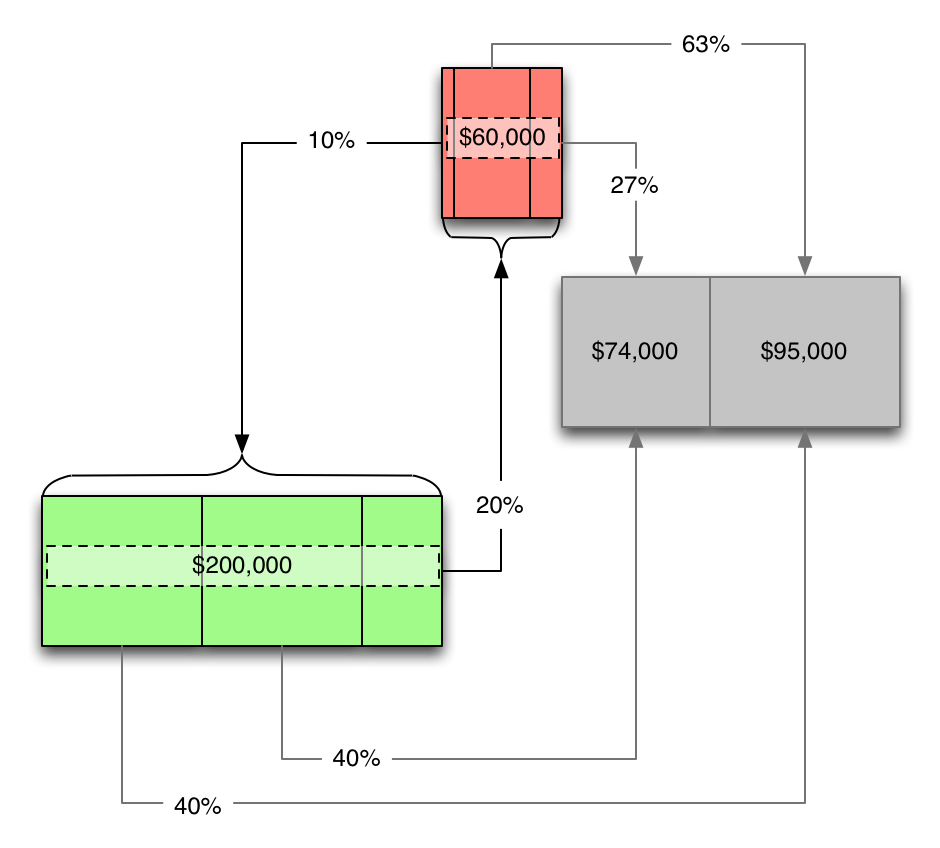
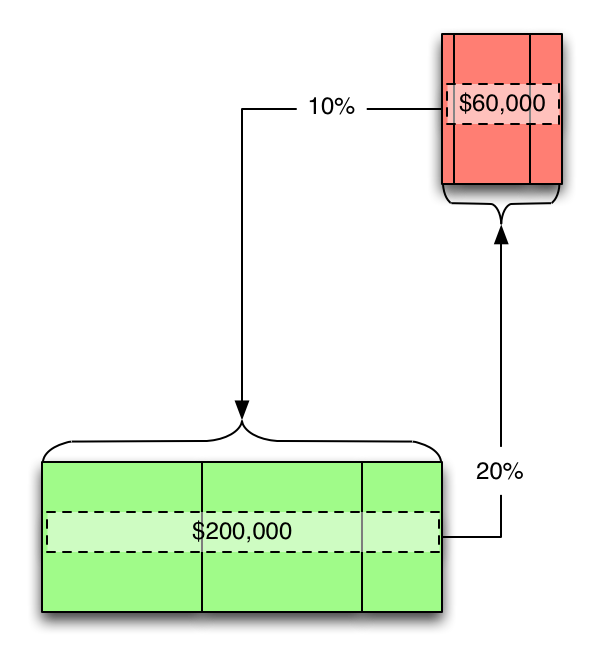
...so we can figure out how they relate to each other:
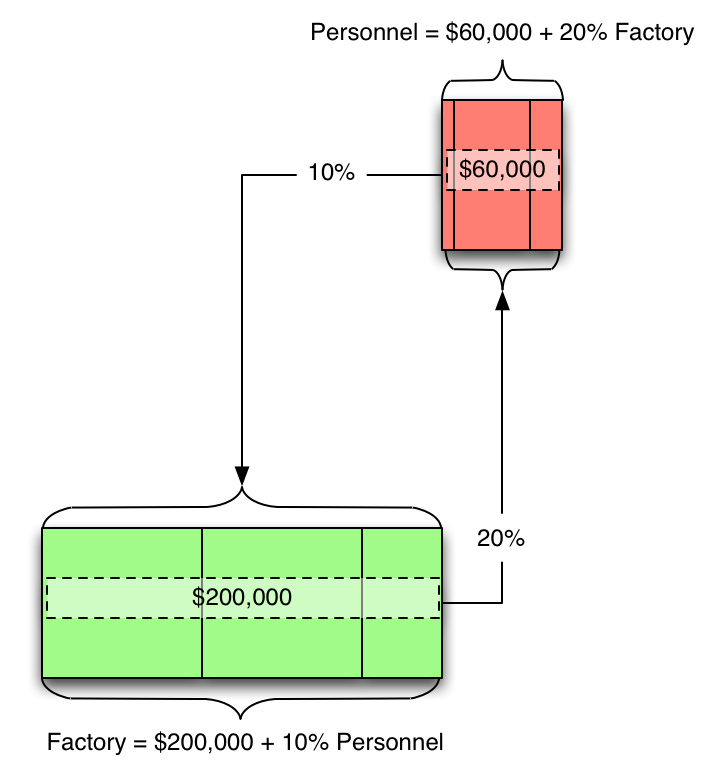
And if we do the algebra:
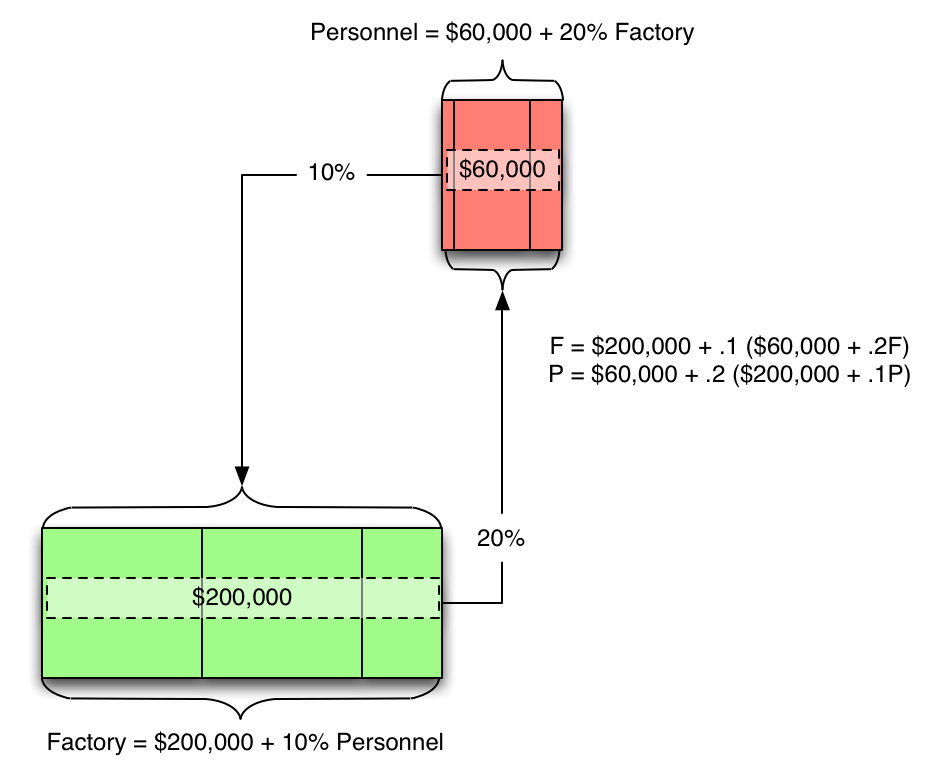
F = $200,000 + .1 ($60,000 + .2F)
P = $60,000 + .2 ($200,000 + .1P)
Where "F" = general factory
And "P" = personnel
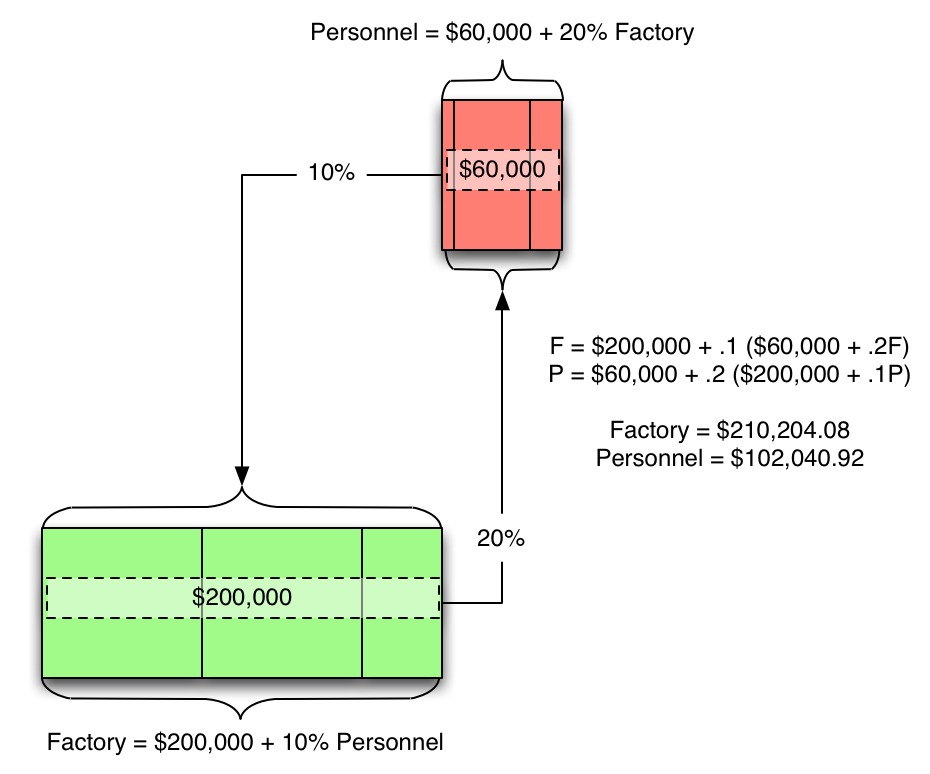
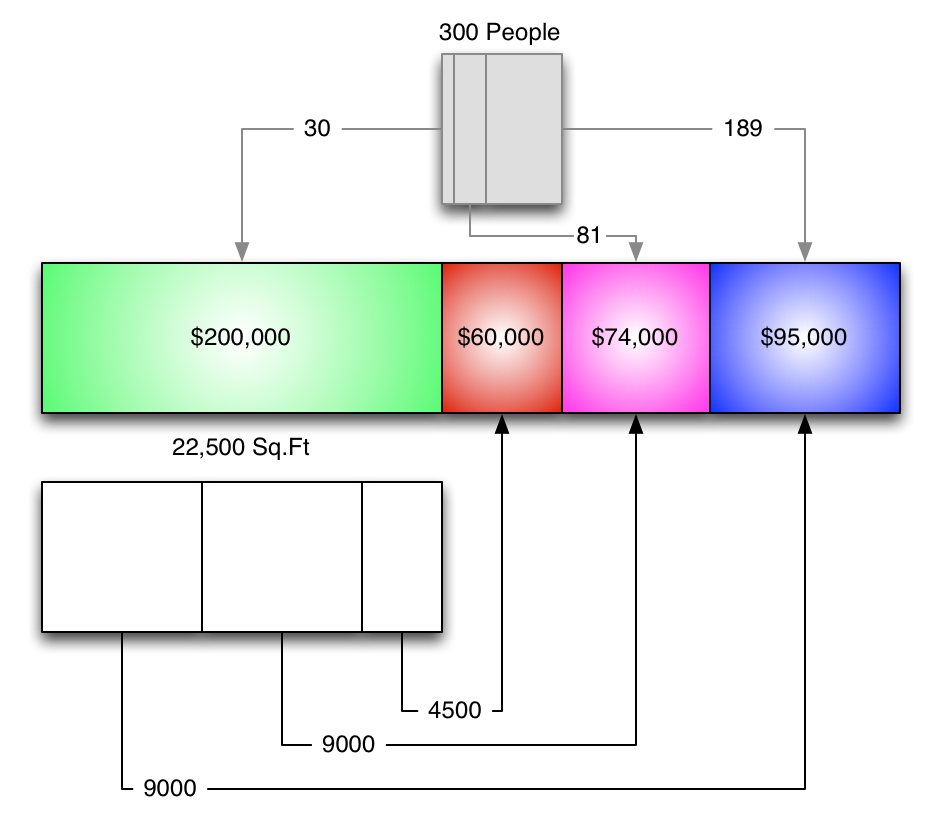
So, let's use those numbers...
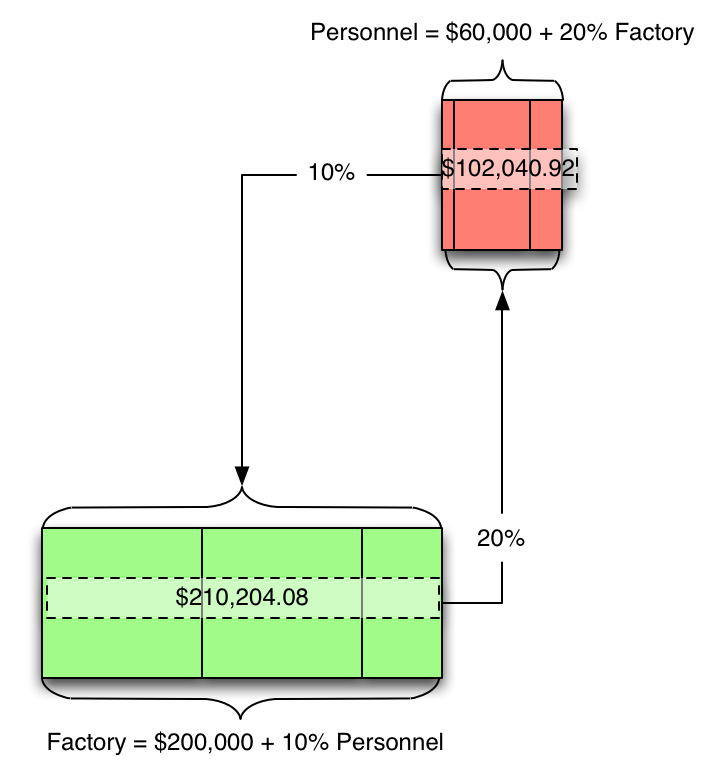
...and bring back the production allocations...
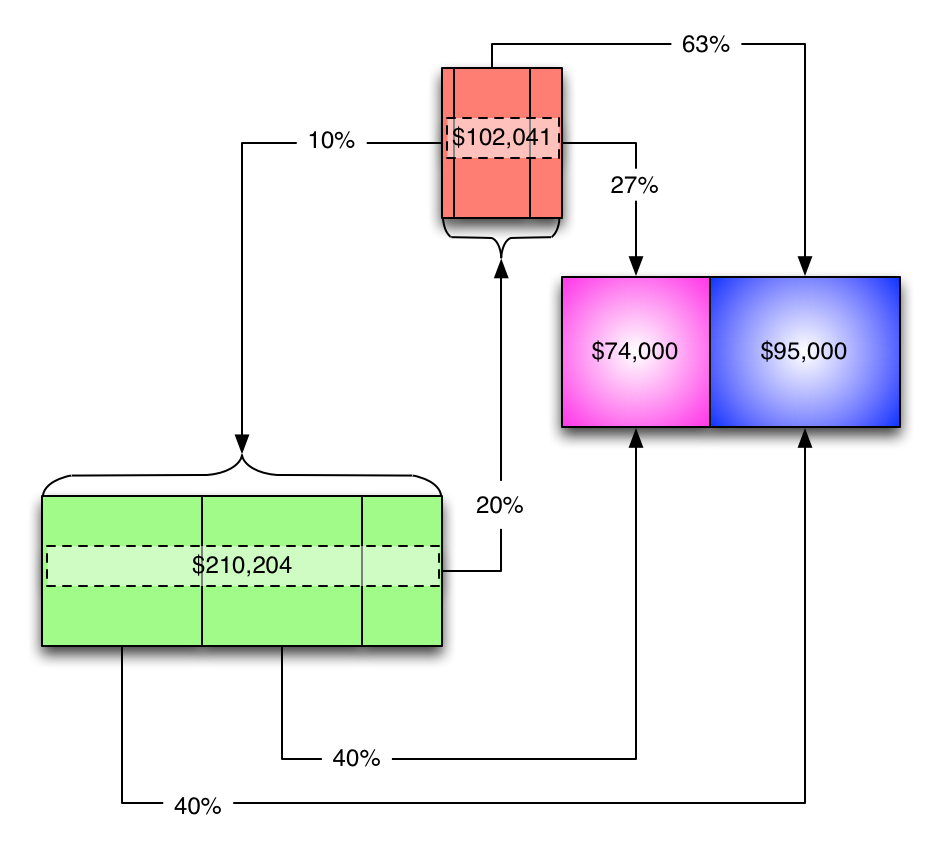
...turn the percentages into dollars...
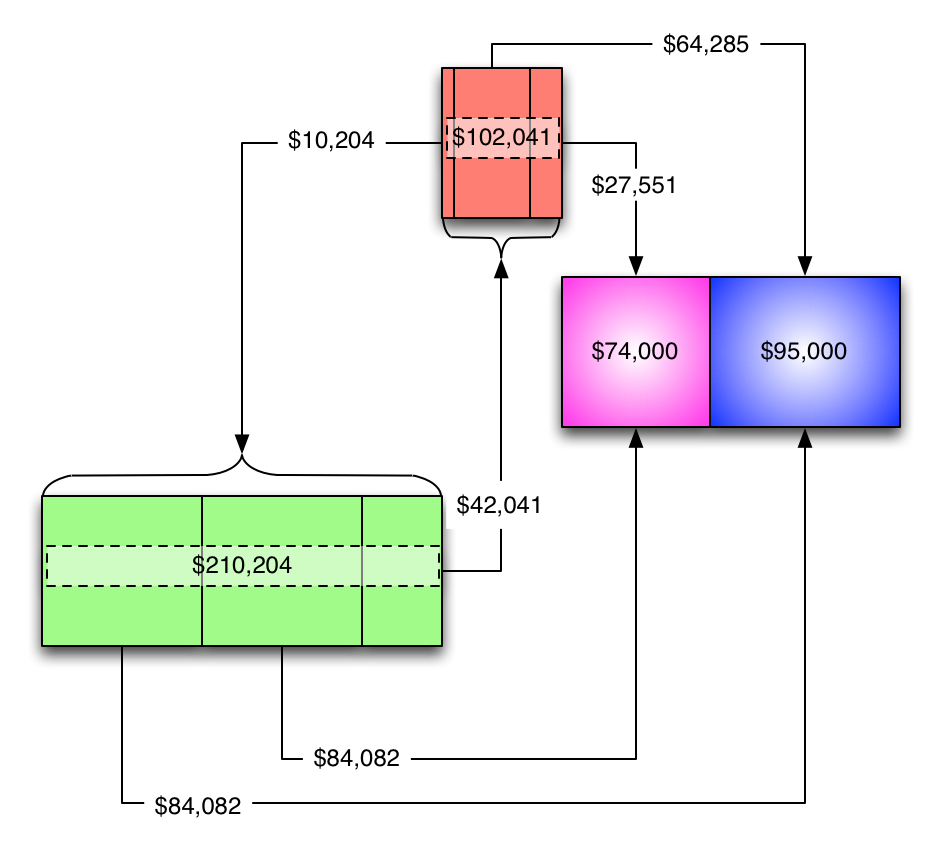
...and remove the service service-to-service lines because they've already been factored in.
(And ajust the scale while we're at it.)
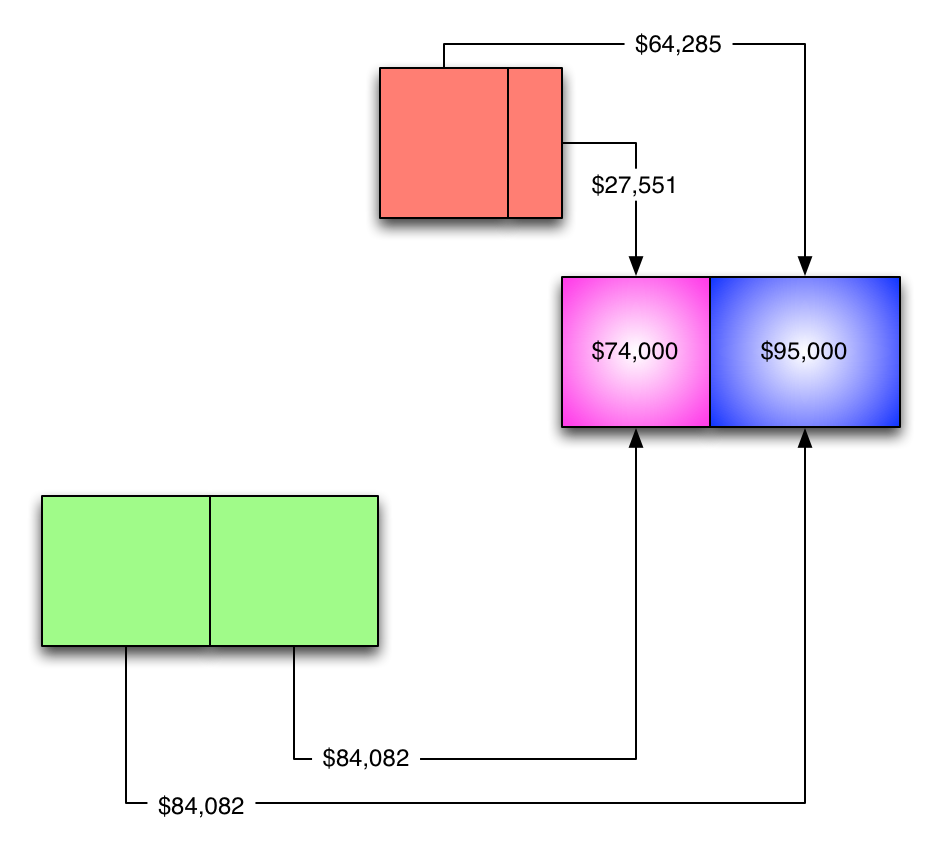
Then we sum up our final allocations.


Now these numbers are pretty good because we didn't fudge anything.
That was the "reciprocal method," and it's the bomb.
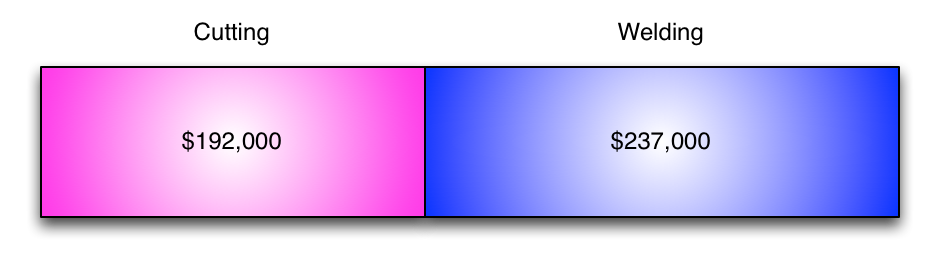
Comparing results looks like this:
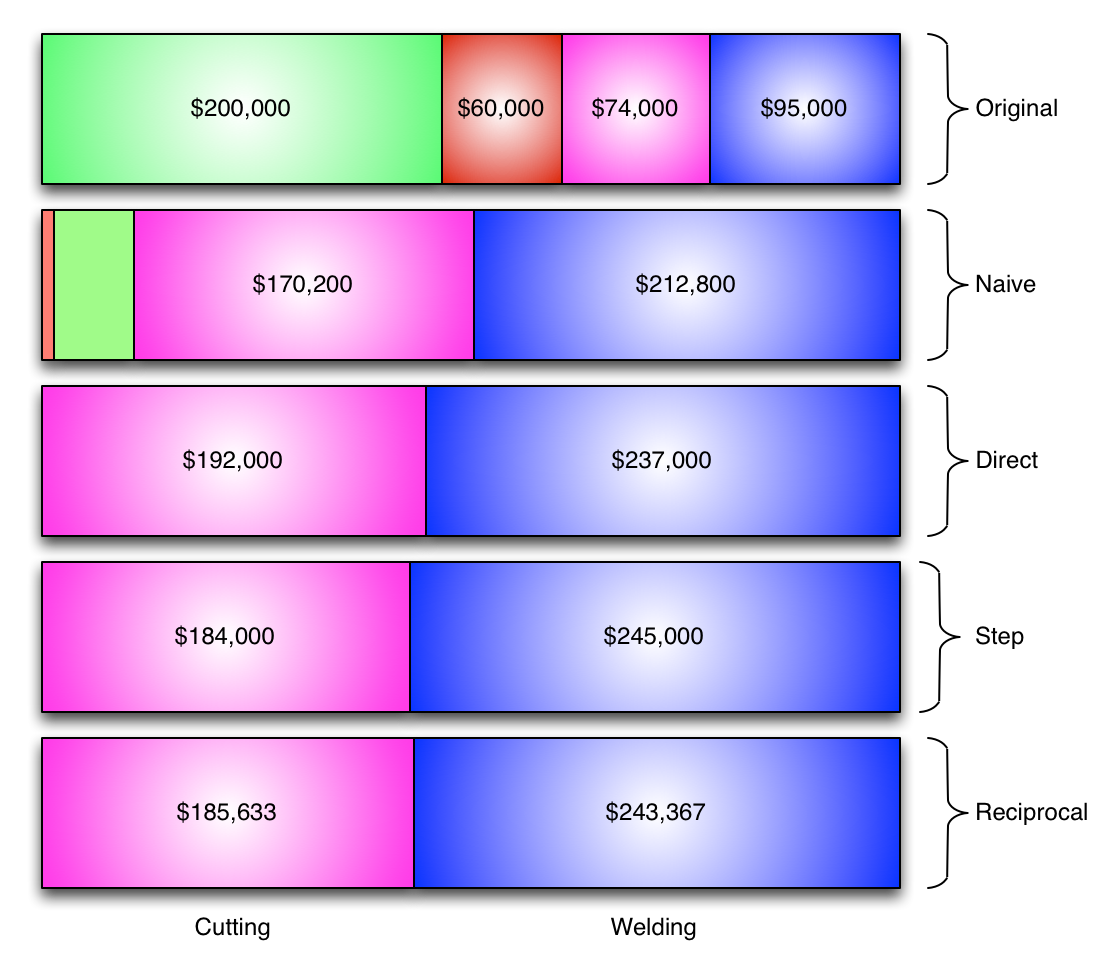
So, we like the reciprocal method because we didn't fudge anything, but it's kind of a PITA isn't it?
I mean seriously, people don't actually do math in the real world, do they?
Well, of course they do silly...
But only if they can't get Excel to do it for them.
Which, in this case, we can.
To begin, copy the data into a new spreadsheet.
Note: H3 contains the equation "=SUM(C3:F3)"
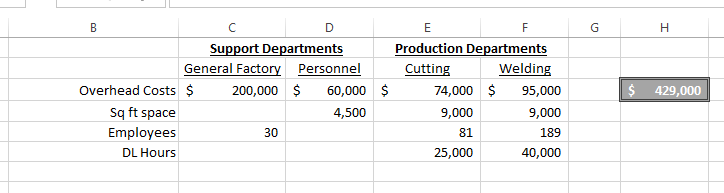
Then we add some summary rows:
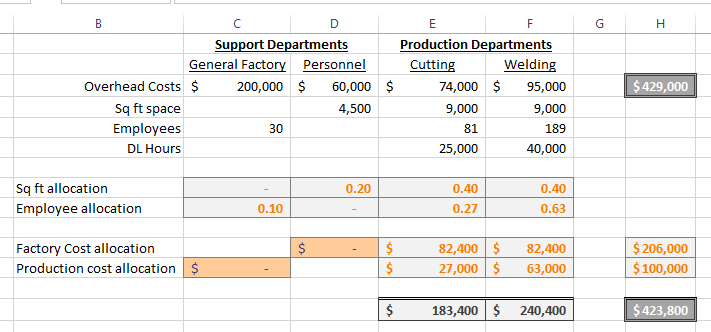
- The two 'allocation' rows (C8:F9) contain the percentages of sqft and employees allocated to each department.
- Cells D11 and C12 (orange backgrounds) are inputs.
- Cell H11 contains "=C3+(C9*C12)"
- Cell H12 contains "=D3+(D8*D11)"
- Cells E11:F12 apply the allocated percentages (E8:F9) of the respective costs to H11:H12.
- Row 14 contains summations.
When H14 and H3 are identical, we have correctly allocated costs.
Didja get that?
Okay, well, here is the source file.
Now you can fire up Solver and tell it to do whatever it takes to Cells D11 and D12 in order to make H3 and H14 equal to one another.
The trick is that D11 must equal H11 and C12 must equal H12.
This is a necessary constraint to ensure that the equations balance correctly.
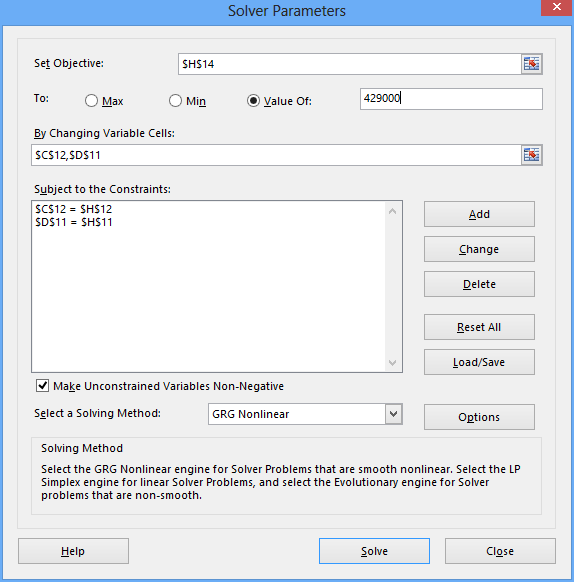
Note that when you tell Solver to set its objective to a specific value, you cannot give it a cell reference.
It's also good practive to tell Solver that the numbers can't be negative, but hey, I'm throwing caution to the wind here.
After telling Solver to solve, we get this:
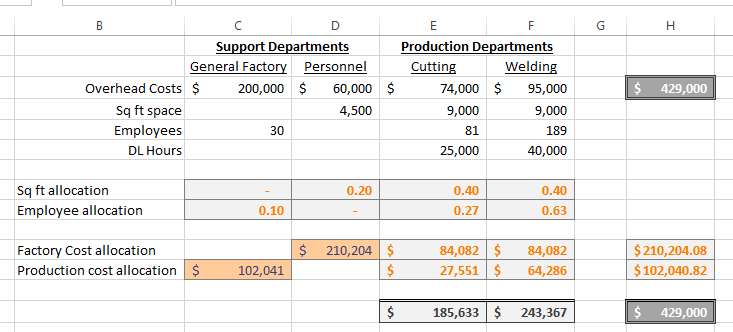
Remarkable! It came up with the same numbers that we did using the algebraic method!
Cells E14 and F14 have the same cost values that we assigned to the purple and blue buckets using the reciprocal method.
And that's pretty much all there is to Awstin Co.
Oh, one more thing...
The worksheet actually asked for the final departmental overhead rates, which is not what we calculated.
To get to the real answer, you must take the summed allocation overhead figures and divide them into the respective labor hour quantities. This will yeild the direct cost per labor hour for each of the production departments.
But you can do that part yourself.